ode45

Syntax

[t,y] = ode45(@func,tin,y0)

[t,y] = ode45(@func,tin,y0,options)

[t,y,te,ye,ie] = ode45(...)

sol = ode45(...)

Inputs

func

The system of equations to solve.

tin

The vector of times (or other domain variable) at which to report the solution. If the vector has two elements, then the solver operates in single step mode and determine the appropriate intermediate steps.

y0

The vector of initial conditions.

options

A struct containing options settings specified via odeset.

The default relative and absolute tolerances are 1.0e-3 and 1.0e-6, respectively.

Outputs

t

The times at which the solution is computed.

y

The solution matrix, with the solution at each time stored by row.

te

The times at which the 'Events' function recorded a zero value, stored as a column vector.

ye

The system function values corresponding to each te value.

ie

The index of the event that recorded each zero value.

sol

A struct containing the solution data. The fields are as follows:

x

The times at which the solution is computed, stored as row vector.

y

The solution matrix, with the solution for each equation in the system stored by row.

solver

The solver name.

xe

The times at which the 'Events' function recorded a zero value.

ye

The system function values corresponding to each xe value.

ie

The index of the event that recorded each zero value.

Example

Find the location in a mass spring damper system:

function dy = MSD(t,y,m,k,c)
  % y = [x, dx/dt]
  dy = [0, 0];
  dy(1) = y(2);
  dy(2) = -y(1)*(k/m) - y(2)*(c/m);
end

v = 1.5;  % initial velocity
m = 1.6;  % mass
k = 1.25; % spring constant
c = 1.1;  % damping constant

handle = @(t,y) MSD(t,y,m,k,c);
t = [0:0.2:12]; % time vector
yi = [0, v];
[t,y] = ode45(handle,t,yi);
x = y(:,1)';
plot(t,x);
xlabel('time');
ylabel('location');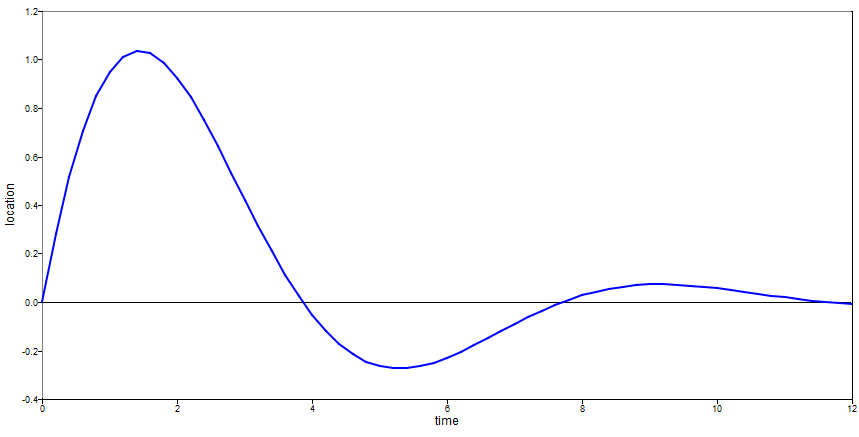

Figure 1. chirp figure 1

Comments

ode45 solves the system with an adaptive Runge-Kutta algorithm the from the Sundials ARKODE library.

To pass additional parameters to a function argument, use an anonymous function.

The 'Events' function used with the last three output arguments is specified using odeset.