fir1
Create a digital FIR filter.
Syntax
[b] = fir1(n,w)
[b] = fir1(n,w,type)
[b] = fir1(n,w,type,window)
[b] = fir1(n,w,type,window,noscale)
Inputs
- n
- The filter order.
- w
- A scalar specifying the cutoff frequency of a low or high pass filter, or a two-element vector specifying the cutoff frequencies of a bandpass or band stop filter, or for a vector containing cutoff frequencies of a multiband filter.
- type
- The band type of the filter. The valid options are:
- 'low' for a low pass filter
- 'high' for a high pass filter
- 'bandpass' for a bandpass filter
- 'stop' for a band stop filter
- 'DC-0' for a multiband filter with a DC value of 0
- 'DC-1' for a multiband filter with a DC value of 1
- window
- A window vector of size n+1. If omitted or [], a Hamming window is used.
- noscale
- Set to 'noscale' if the output is not to be normalized. When
omitted, the gain is set to 1 as follows:
- At DC for 'low'
- At the Nyquist frequency for 'high'
- At the center of the pass band for 'bandpass'
- At DC for 'stop'
- At the center of the first pass band for 'DC-0'
- At DC for 'DC-1'
Outputs
- b
- The polynomial coefficients of the filter.
Example
Plot the magnitude response in decibels for a 50th order FIR low pass digital filter with a 250 Hz cutoff frequency and a 2000 Hz sampling frequency.
w = hamming(51, 'symmetric');
fc = 250;
fs = 2000;
num = fir1(50,fc/(fs/2),'low',w);
[h,f] = freqz(num,1,[0:5:1000],fs);
plot(f,20*log10(abs(h)));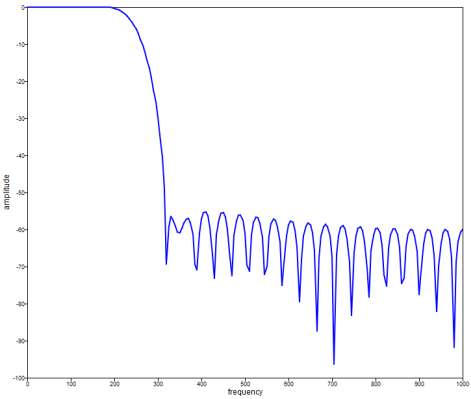
Figure 1. fir1 figure 1
Example 2
Plot the magnitude response in decibels for a 50th order FIR multiband digital filter with passbands of [300,400], [590,610], [775,825], and a 2000 Hz sampling frequency.
w = hamming(51, 'symmetric');
fc = [300,400,590,610,775,825];
fs = 2000;
num = fir1(50,fc/(fs/2),'DC-0',w);
[h,f] = freqz(num,1,[0:5:1000],fs);
plot(f,20*log10(abs(h)));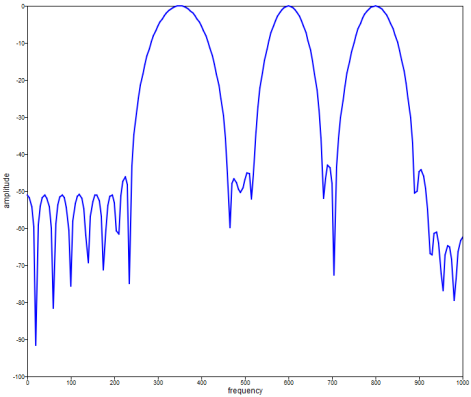
Figure 2. fir1 figure 2
Comments
The filter order must be even for highpass or band stop filters. The function increments an invalid odd order automatically when the default window is used.